درباره من
عمر شما از زمانی شروع می شود که اختیار سرنوشت خویش را در دست می گیرید
ادامه...
روزانهها
همهپیوندها
- درس شیرین ریاضی
- دانلود فلش کارت
- خدمات الکترونیکی راهنمایی و رانندگی صدور عدم خلافی و نمره منفی و پیگیری مدارک و ...
- آموزش ریاضی همراه با بازی
- مدرسه عشق (آقای عبدالعلی پور) مدرسه خیر آباد
- Beat The Gmat
- حرف هایی از جنس ناچاری
- بلاگ اسکای
- لبخند ریاضی
- همه نوع کمک در باره کامپیوتر و موبایل
- آموزش ریاضی چناران
- ریاضی را با بازی بیاموزید
- ریاضیات علم برتر(آقای صبحی)
- تجارب یادگیری-یاددهی(آقای هادیفرد)
- سیمیای ادب(آقای دلگشای)
- وبلاگ آقای صالح قرنی
- مکمل کلاس ریاضی
- نرم افزار های آموزش ریاضی
- خرید ارزان نرم افزار های آموزش ریاضی
- مرجع MBA
- آموزش والیبال تبریز
- مشاوره MBA
- وبلاگ دانش آموز عزیز رحیم حاجبی
- ثبت لینک شما در 150 موتور جستجوگر
- فلش های آموزشی
- MBA تبریز
- مدرسه اینترنتی
- گروه های آموزشی آذربایجان شرقی
- (ویژهی دانشآموزان راهنمایی و دبیرستان)
- المپیاد ریاضی راهنمایی
- انجمن MBA ایران
- محمد رضا ناصر زاده (زبان)
- دندان پزشکی ( امین وحدتی)
- امیر عرفانیان (GMAT)
- مسعود آقاسی (ریاضی)
- رنک گوگل
- کنکور و رشتهMBA
- موسسه آموزش آزاد پِژوهش
- احمد صداقت (GMAT)
- برترین های MBA
- موسسه آموزش عالی بهار (MBA)
- ریاضی را آسان بگیریم
- دانلود جدیدترین فیلم ها
- گروه ریاضی ترکمنچای (امیر ابراهیمی)
- آزمون آنلاین گروه های آموزشی آذربایجان شرقی
- مرجع مدیریت اجرایی
- مدیریت اجرایی
- بانک فلش کارت
- آموزش ریاضی ارشد ( وحید انصاری)
- ارشد و دکترا
- وبسایت تخصصی دکترا
- استعداد تحصیلی
- هادی مسیح خواه
- جویامجد تهران
- سایت کمک آموزشی چمپا
- اندیشه ریاضی (معمای روزانه)
- Gmat Club
- ریاضت 20
- اعزام به خارج
- مرکز امور بین الملل و مدارس خارج از کشور
- رهروان ولایت
- فرهنگیان نیوز خبرگزاری فرهنگیان
- سازمان مدیریت صنعتی MBA و تحقیق و مشاوره
- ریاضی هفتم
- قالب های آماده پاور پوینت
- ام بی ای آنلاین
- مهندس وحید انصاری
- بی هم نفس
جدیدترین یادداشتها
همه- 6 رابطه ریاضی در نماز های یومیه
- نمونه سوال ریاضی خرداد ماه 94 پایه هفتم و هشتم
- آیا می خواهید یک عدد 99 رقمی را بخوانید و از خواندن خود لذت ببرید
- مدیر از دنیا رفته
- روش ساخت دستگاه برش حرارتی
- هــــرگز نکنم شکـــوه و ناله نه گلایه
- دانلود رایگان نمونه سوالات خرداد سوم راهنمایی و هفتم متوسطه
- وعده نده لطفا !!!
- عدد طلایی(Golden number)
- 30 معمای جالب و فکری
- سرفصل ریاضی هفتم (اول متوسطه 1)
- تاریخچه ریاضی
- کاربرد ریاضی در زندگی
- روشهای جالب برای ضرب و تقسیم
- بوروکراسی های امروزی و مدیران بروز
- دانلود رایگان سوالات ارشد 92
- طرح درس رابطه فیثاغورس
- آموزش مبحث مبنا از کتاب ریاضی دوم راهنمایی
- عشق چیست؟؟؟ اگه اینو بخونین ببینم بازم می گین استادا دل ندارن!
- کشف معجزه ریاضی قرآن از طریق کامپیوتر
- ایام عزاداری محرم تسلیت باد
- معمای انیشتین !(آیا شما جزو 2 درصد باهوش ها هستید)
- آخرای تابستان با یک معمای خوب
- آیا مشکل همه دانش آموزان 5=2*2 می باشد
- صدای اذان در طول 24 ساعت روی کره زمین قطع نمی شود
- 65=64
- نمونه سوالات امتحانی خرداد ماه درس ریاضی مقطع راهنمایی
- دو داستان واقعا آموزنده و با ارزش
- مساحت و محیط اشکال هندسی
- یک واقعیت همیشگی
- چند سوال هوش ریاضی میزارم حال کنین
- اعداد گنگ (Irrational numbers)
- دانلود رایگان نمونه سوالات نیمسال اول 91-90 دانشگاه پیام نور
بایگانی
- آبان 1395 1
- فروردین 1394 1
- اسفند 1393 1
- دی 1393 1
- آذر 1393 1
- مرداد 1393 1
- فروردین 1393 1
- اسفند 1392 1
- بهمن 1392 1
- مهر 1392 1
- مرداد 1392 1
- فروردین 1392 3
- اسفند 1391 1
- بهمن 1391 1
- دی 1391 1
- آذر 1391 3
- آبان 1391 1
- مهر 1391 1
- شهریور 1391 3
- تیر 1391 1
- اردیبهشت 1391 1
- فروردین 1391 2
- اسفند 1390 4
- بهمن 1390 5
- دی 1390 8
- آذر 1390 1
- آبان 1390 5
- مرداد 1390 1
- خرداد 1390 1
- اسفند 1389 1
- بهمن 1389 4
تقویم
آبان 1395| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
جستجو
آمار بازدید : 156337 بازدید
Powered by Blogsky
قضیه فیثاغورث
د رمثلث قائمالزاویه زیر رابطهی زیر همیشه بین اضلاع برقرار است:
![]()
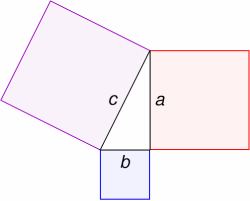
میتوان این قضیه را به صورت سادهتر بیان کرد : فرض کنید سه مربع روی اضلاع یک مثلث قائم الزاویه،که طول اضلاع قائم آن a وb و طول وتر آن c میباشد؛مطابق شکل زیر میسازیم
این قضیه به ما توضیح میدهد که جمع مساحتهای دو مربع ساخته شده روی دو ضلع قائم یک مثلث قائم الزاویه با مساحت مربع ساخته شده روی وتر برابر است.
مثلث قائم الزاویه مثلثی است که دارای یک زاویه قائم میباشد و به ضلعی که روبروی این زاویه در مثلث قرار دارد، وتر میگویند.
در شکل اضلاع زاویه قائم با aوb و وتر با c نشان داده شده است.
بیان دیگر قضیه به این صورت است که در یک مثلث قائم الزاویه مجموع مربعات دو ضلع قائم با مجذور وتر برابر است.
جالب است بدانید که بیش از شصت روش هندسی برای اثبات این قضیه وجود دارد.
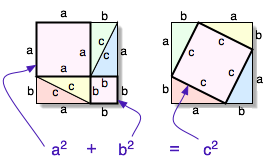
می توان با توجه به شکل روبرو اثبات هندسی قضیه را به راحتی درک کرد.
در هر دو شکل مربعی به ضلع a+b داریم.در شکل سمت راست چهار نمونه از مثلث قائم الزاویه دور مربع ساخته شده بروی وتر وجود دارد. و هر چهار مثلث دارای مساحت یکسان می باشند. با چند جابجایی در شکل سمت راست به شکل سمت چپ میرسیم.در این شکل همان چهار مثلث قبلی وجود دارند ولی مربعی که اضلاع آن به c بود به دو مربع به اضلاع a,b تبدیل شده است، که همان قضیه فیثاغورث را نشان میدهد
در هر دو شکل مربعی به ضلع a+b داریم.در شکل سمت راست چهار نمونه از مثلث قائم الزاویه دور مربع ساخته شده بروی وتر وجود دارد. و هر چهار مثلث دارای مساحت یکسان می باشند. با چند جابجایی در شکل سمت راست به شکل سمت چپ میرسیم.در این شکل همان چهار مثلث قبلی وجود دارند ولی مربعی که اضلاع آن به c بود به دو مربع به اضلاع a,b تبدیل شده است، که همان قضیه فیثاغورث را نشان میدهد
رضا
جمعه 23 دیماه سال 1390 ساعت 13:51
لطفا توضیح دهید اینکه یه بنا از قضیه فیثاغورث استفاده می کند چگونه است؟
قضیه فیثاغورس میگه اگه اندازه یک ضلع زاویه قائمه 6 و اندازه ضلع قائمه دیگر 8 باشد آنگاه اندازه وتر 10 می باشد و بنا ها ابتدا از دیوار 60 سانتی متر اندازه می گیرند و سپس از زمین به طول 80 سانتی متر اندازه می گیرند و در آخر فاصله انتهای دو اندازه ی گرفته شده را متر می کنند اگر یک متر باشد می گویند قائم است اگر بیش از یک متر باشد دیوار رو به بیرون و اگر کمتر از یک متر باشد دیوار رو به داخل خم دارد
فقط همین سه تا عدد کاربرد داره دیگه نه؟
نه خیر هر عددی که در رابطه صدق کنه درسته اینایی که من گفتم به غلت سر راست بودن بیشتر مورد استفاده واقع می شوند